编程公式

求一个数的位数公式

作用

快速的求一个数n的位数，比如345 --> 3位。

公式

$$(int)log10(n)+1$$

斯特林公式

作用

快速求一个数n阶乘的近似值，n越大越近似。

公式

$$n!\approx\sqrt{2*n*π}(n/e)^{n}$$

卡特兰数

作用

求n个节点的二叉树共有几种形态

公式

$$f\left( n \right) = \left( 2n \right)!/n!\left( n+1 \right)!$$

牛顿迭代

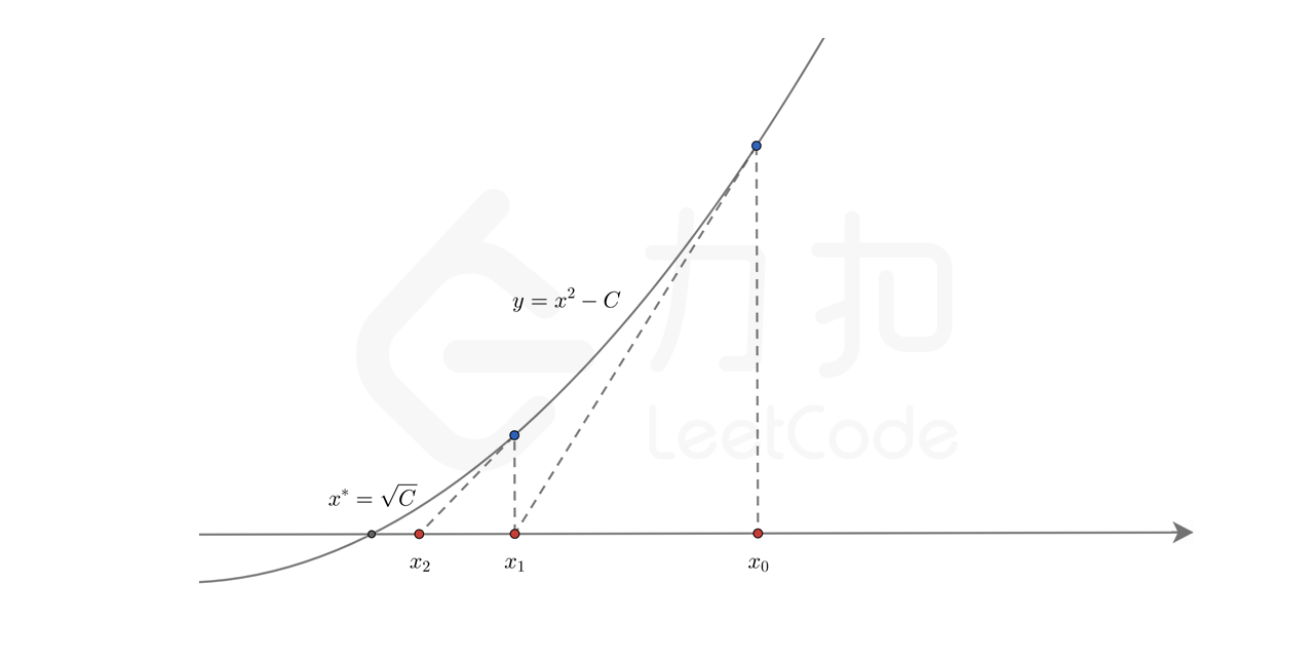
牛顿迭代是一种可以用来快速求解函数零点的方法

$$y = f(x) = x^{2} - C$$

我们可以用C表示待求出平方根的那个整数，显然C的平方根就是上述函数的零点。

牛顿迭代法的本质是借助泰勒级数，从初始值开始快速向零点逼近。开始可以任取一个Xo作为初始值。如下图：

代码

class Solution {
    public int mySqrt(int x) {
        if(x == 0) return 0;
        double C = x;
        double x0 = x;
        while(true) {
            double x1 = 0.5 * (x0 + C / x0);
            if(Math.abs(x0-x1) < 1e-7) break;
            x0 = x1;
        }
        return (int)x0;
    }
}

埃式筛选

质数：是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。又称素数。例如2， 3， 5， 7等。否则称为合数。其中1既不是质数也不是合数。

埃式筛（Sieve of Eratosthenes）是一种高效的素数筛选算法，用于找出某个范围内的所有素数。它的基本思想是通过不断标记合数来排除非素数，最终留下的未标记数即为素数。

步骤说明：

• 初始化一个数组： 创建一个从 2 到目标数字 n 的布尔数组 isPrime，初始值全为 true，表示所有数都可能是素数。
• 标记非素数： 从第一个素数 2 开始，标记所有 2 的倍数为非素数（将 isPrime[i] 设置为 false）。然后找到下一个未被标记的数（即下一个素数），重复这个过程。
• 停止筛选： 当标记到的数大于或等于 Math.sqrt(n) 时，可以停止筛选，因为更大的数的倍数已被标记。
• 提取素数： 数组中剩余值为 true 的位置对应的数就是素数。

function sieveOfEratosthenes(n) {
    // 初始化布尔数组，表示所有数可能都是素数
    const isPrime = Array(n + 1).fill(true)
    // 0 和 1 不是素数
    isPrime[0] = isPrime[1] = false 
    // 从 2 开始筛选，直到 sqrt(n)
    for (let i = 2; i * i <= n; i++) {
        if (isPrime[i]) {
            // 将 i 的倍数标记为非素数
            for (let j = i * i; j <= n; j += i) {
                isPrime[j] = false
            }
        }
    }
    // 提取素数，过滤出 isPrime 中值为 true 的下标
    return isPrime
        .map((prime, index) => (prime ? index : null))
        .filter((number) => number !== null)
}
// 测试：获取 50 以内的所有素数
console.log(sieveOfEratosthenes(50))

2的幂

如何快速判断一个数(n)是不是2的幂

如果一个数是 2 的幂，则它的二进制表示中首位是 1，其余都是 0

4 --> 100
8 --> 1000
16 --> 10000

// 判断n是否为2的幂
如果 n&(n-1) == 0 则是2的幂

三角形面积公式

普通公式

三角形的面积S等于底边长a乘以该边上的高h再乘1/2

$$\frac{a * h}{2}$$

海伦公式

已知三角形的三边长为a, b, c

$$p = \frac{a + b + c}{2}$$

$$S = \sqrt{p(p-a)(p-b)(p-c)}$$

行列式

已知三角形三个顶点坐标为(x₁, y₁)、(x₂, y₂)、(x₃, y₃)

$$S = \frac{1}{2} \left| \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} \right|$$

判断两个字符串是否有相同字符

方法一 数组

// str1和str2字符串都是小写的英文字母
// 如果str1和str2有重复返回true否则返回false
public boolean allowDuplicates(String str1, String str2) {
    // 用数组下标0~25分别对应a~z
    int[] arr = new int[26];
    for(int i = 0; i < str1.length(); i++) {
        // 将str1中每个字符对应的数组下标设为1
        arr[str1.charAt(i) - 'a'] = 1;
    }
    for(int i = 0; i < str2.length(); i++) {
        // 判断str2，如果str2中的字符对应下标已经在数组中存在(等于1)则返回ture说明有相同字符
        if(arr[str2.charAt(i) - 'a'] == 1) return true;
    }
    return false;
}

方法二 位掩码

// 如果str1和str2有重复返回true否则返回false
public boolean bitMask(String str1, String str2) {
    int str1BitMask = 0;
    int str2BitMask = 0;
    for(int i = 0; i < str1.length(); i++) {
        str1BitMask |= (1 << (str1.charAt(i) - 'a'));
    }
    for(int i = 0; i < str2.length(); i++) {
        str2BitMask |= (1 << (str2.charAt(i) - 'a'));
    }
    return (str1BitMask & str2BitMask) != 0;
}

// str1.charAt(i) - 'a' 
// 解释：Java做字符的加减法时会把字符转为ASCII码进行计算，a的ASCII码是97。如果str1.charAt(i) = ‘c’ 则str1.charAt(i) - 'a' = 99 - 97 = 2

// 1 << (str1.charAt(i) - 'a')
// 解释：Java中 << 表示二进制左移，1 << 2 在二进制中表示将数字1左移两位。左移操作符<<会将数字的二进制形式向左移动指定的位数，并在右边补0。1 << 2可以表示为把1的二进制0001中的1左移两位得到0100。

// str1BitMask |= (1 << (str1.charAt(i) - 'a'));
// 解释：如果开始str1BitMask = 0001，(1 << (str1.charAt(i) - 'a')) = 0100。则str1BitMask |= (1 << (str1.charAt(i) - 'a')) = 0001 | 0100 = 0101。作用就是把原来含有的字符和当前字符合并。

// 如果最终str1BitMask = 0101，对0101观察发现第一位(从右到左)和第三位是1，就表示str1中有a和c。如此就可以用26个二进制位表示一个字符串含有的字符。第一位(从右到左)是1则表示含有a，第二位(从右到左)是1则表示含有b，以此类推。

// str1BitMask & str2BitMask
// 解释：如果(str1BitMask & str2BitMask == 0)则表示没有相同的字符。
// 例子：如果str1 = "acd",则str1BitMask = 1101。str2 = “bef”，则str2BitMask = 110010。1101&110010是等于0的表示没有相同字符。